简述
本文记录我记录我学习 坐标体系和矩阵转换的过程,加深学习便于后续查询,可能有些描述不够准确,或者内容不够充实,还请多多指正,共同学习.
颜色
一个没有Alpha通道的颜色可以用一个3维向量来表示 例如 glm::vec3(1.0,1.0,1.0); 表示白色.
在现实世界中,一个物体的颜色是它反射的颜色导致的, 例如我们将纯红光 照射在纯绿物体上, 因为红光都被吸收,所以显示为黑色.
将吸收反射的过程用向量表示出来
1 | glm::vec3 lightColor(0.0f, 1.0f, 0.0f); //绿色光源向量 |
冯氏光照模型
冯氏光照模型的主要结构由3个分量组成 环境(Ambient) 漫反射(Diffuse) 镜面(Specular)
环境光照
在现实环境下 即使在黑暗的情况下,世界上通常也会有一些光亮(如 月光), 而且即使物体不朝光源的,也会因为 其他物体的反射,使阴面有光,这种情况下 就要使用 全局照明算法 这种算法开销大而且复杂,以后在研究 先实现简单的 环境光照
所以给物体一个环境光照量,让物体始终有一点颜色. 在着色器中表现如下
1 | void main() |
漫反射光照
模拟光源对物体的方向性影响(Directional Impact)。它是冯氏光照模型中视觉上最显著的分量。物体的某一部分越是正对着光源,它就会越亮. 也就是光线和物体表面法线的夹角越小,光线对物体的影响就越大.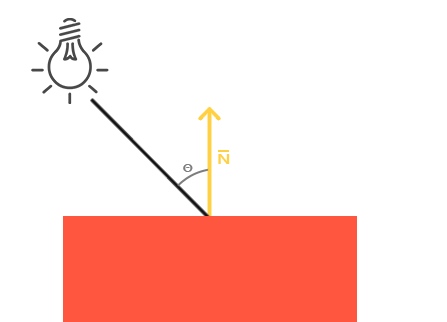
这样就可以利用夹角的cos值作为参考,来修改光线对物体的影响.
片段着色器重相关实现1
2
3
4
5
6uniform vec3 lightColor; //光源色
uniform vec3 lightPo; //光源位置
uniform vec3 objectColor; //物体色
uniform vec3 viewPo; //物体位置
in vec3 outNormal; //传入当前顶点平面的法向量
1 | vec3 norm = normalize(outNormal); //确保法线为单位向量 |
法向量变换
对于法向量,它是一个方向向量,不会因为物体的移动而发生变化,所以在对法向量 进行矩阵处理时,要消除矩阵中位移部分对其造成的影响. 因此位移使用3x3矩阵 或者 将 法向量的w分量设置为0.0;
另外,若矩阵对物体进行里不等比缩放时候,会导致法向量不在垂直于物体表面.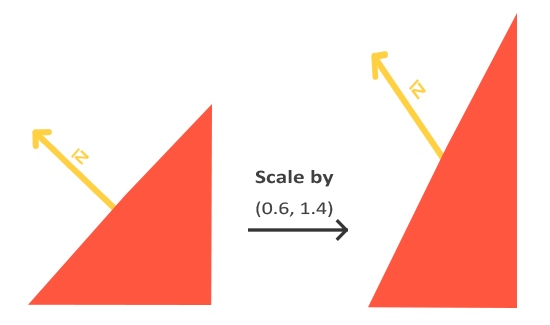
这种情况 则需要使用法线矩阵 来移除对法向量错误缩放的影响. 法线矩阵由逆矩阵和转置矩阵 组成.
1 | glm::transpose(glm::inverse(model)); //法线矩阵的计算 |
镜面光照
模拟有光泽物体上面出现的亮点。镜面光照的颜色相比于物体的颜色会更倾向于光的颜色。镜面光照的计算依赖于 观察的视角, 若视线与光源在物体的反射线的夹角越小 则镜面光照效果越好.
计算他 我们需要 观察者位置.镜面强度(镜面效果强弱)
1 | float specularStrength = 0.5; //镜面强度 |
256 表示高光的反光度, 反光度越高,发射光的能力越强,散射越少 高光点越小
最后综合
1 | vec3 res =(ambientStrength + diffuse + specular) * objectColor; |
效果图: 白色方块为白色光源